martes, 11 de marzo de 2014

CLASIFICACION DE POLIGONOS

 Podemos clasificar a los polígonos en regulares e irregulares, fijándonos en sus lados y, en cóncavos o convexos, fijándonos en sus ángulos.









Polígonos Regulares

Son todos los polígonos cuyos lados y ángulos son iguales.
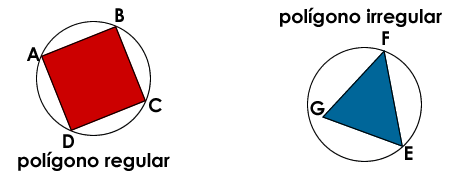
Una característica particular de los polígonos regulares, es que siempre pueden ser inscritos en una circunferencia.
Por ejemplo, un cuadrado es un polígono regular de 4 lados. Si te fijas en el dibujo que está a continuación, podrás ver que todos sus puntos (A, B, C, D) tocan a la circunferencia, sin embargo, en el triángulo que está al lado, sólo dos de sus puntos tocan a la circunferencia (E, F), lo que nos muestra que es un polígono irregular.







Polígono Irregular:

Decimos entonces que un polígono es irregular cuando sus lados no son iguales, y podemos ver también, que no todos sus puntos tocan la circunsferencia.

Polígonos Cóncavos y Convexos

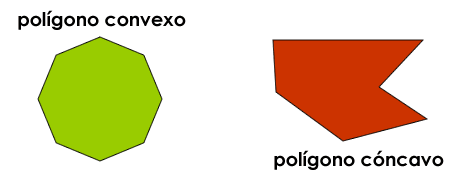
Un polígono es convexo si todos sus ángulos interiores son menores de 180º y decimos que es un polígono cóncavo si al menos uno de sus ángulos interiores mide más de 180º.







MODELOS MATEMÁTICOS PARA DETERMINAR ÁNGULOS Y DIAGONALES EN POLÍGONOS CONVEXOS

Las diagonales son las lineas que van de vertice a vertice sin que estos sean continuos... por ejemplo... el triangulo no tiene diagonales... el cuadrado tiene 1 desde un vertice y 2 desde todos los vertices... sin que se repitan las diagonales... el pentágono desde un vertice tiene dos pero si contamos todas las diagonales.... sin que se repita alguna son 6... 


los angulos internos de un poligono son aquellos que se forman con dos lados del mismo polígono... 


las diagonales desde un vertice se obtienen con la formula... n - 3 

las diagonales totales de un poligono se obtienen con la formula ( n(n - 3) ) / 2 

los angulos internos de un poligono se obtienen con la sig. formula ( 180(n - 2) ) / n 

donde n = numero de lados 


DEMOSTRACIONES



CALCULO DE DIAGONALES 





COMO SACAR LAS AREAS DE POLIGONOS REGULARES


En función del perímetro y la apotema[editar]



El área de un polígono regular, conociendo el perímetro y la apotema es:
A = \frac {P \cdot a}{2}
] Demostración
  • Partiendo del triángulo que tiene por base un lado L, del polígono y altura su apotema a , el área de este triángulo, es:
A_t = \frac{L \cdot a}{2} \;
  • Un polígono de n lados, tiene n de estos triángulos, por lo tanto el área del polígono será:
A_p = \frac{L \cdot a}{2} \cdot n \;
  • Sabiendo que la longitud de un lado L, por el número n de lados, es el perímetro P, tenemos:
A_p = \frac{P \cdot a}{2} \;



Circunferencia y círculo como lugares geométricos

Un LUGAR GEOMÉTRICO es un conjunto de puntos que cumplen una determinada condición.
• Circunferencia es el lugar geométrico de los puntos del plano que se encuentran a la misma distancia de otro que vamos a llamar centro.

• Círculo es el lugar geométrico de todos los puntos que equidistan del centro y todos los puntos cuya distancia al centro es menor que aquélla.

TEOREMAS DE ANGULOS DENTRO Y FUERA DE LA CIRCUNFERENCIA

1 Ángulo central

dibujo
El ángulo central tiene su vértice en el centro de la circunferencia y sus lados son dos radios.
La medida de un arco es la de su ángulo central correspondiente.
expresión

2 Ángulo inscrito

dibujo
El ángulo inscrito tiene su vértice está en la circunferencia y sus lados son secantes a ella.
Mide la mitad del arco que abarca.
expresión

3 Ángulo semi-inscrito

dibujo
El vértice de ángulo semiinscrito está en la circunferencia, un lado secante y el otro tangente a ella.
Mide la mitad del arco que abarca.
expresión

4 Ángulo interior

dibujo
Su vértice es interior a la circunferencia y sus lados secantes a ella.
Mide la mitad de la suma de las medidas de los arcos que abarcan sus lados y las prolongaciones de sus lados.
expresión

5 Ángulo exterior

Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son: o secantes a ella, o uno tangente y otro secante, o tangentes a ella:
dibujodibujodibujo
Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son: o secantes a ella, o uno tangente y otro secante, o tangentes a ella:
expresión

CALCULO DE AREA Y PERIMETRO DEL CIRCULO

Circunferencia: 
Área = π*r^2 
Perimetro = 2*π*r 

donde: 
r: radio de la circunferencia 
π: (pi) es un número irracional, cociente entre la longitud de la circunferencia y la longitud de su diámetro. Se emplea frecuentemente en matemática, física e ingeniería. El valor numérico de π truncado a sus diez primeras posiciones decimales, es el siguiente: 

π = 3.1415926535 

VOLUMENES

Volumen del cubo

cuboEl volumen del cubo equivale a la longitud de su cara a tercera potencia.
Formula volumen de cubo
V = 
a
3

donde 
V
 - cubo volumen,
a
 - longitud de la cara del cubo.Vea también online calculadora para sacar volumen del cubo.


Volumen de la prisma

prismaEl volumen de la prisma equivale a la multiplicación del área de la base en la altura.
Formula volumen de prisma

V = 
Ab h

donde 
V
 - prisma volumen,
Ab
 - área de las bases de la prisma,
h
 - longitud de la altura de la prisma.


Volumen del paralelepípedo

paralelepípedoVolumen del paralelepípedoequivale a la multiplicación del área de la base por la altura.
Formula volumen de paralelepípedo
V = 
Ab · h

donde 
V
 - paralelepípedo Volumen,
Ab
 - área de las bases de la paralelepípedo,
h
 - longitud de la altura de la paralelepípedo.Vea también online calculadora para sacar volumen del paralelepípedo.


volumen del ortoedro

ortoedroOrtoedro volumen equivale a la multiplicación de su longitud, latitud y altura.
Formula volumen de ortoedro

V = 
a · b · h

donde 
V
 - ortoedro volumen,
a
 - longitud,
b
 - latitud,
h
 - altura.Vea también online calculadora para sacar volumen del ortoedro.


Volumen de la pirámide

pirámideEl volumen de la pirámide equivale a la tercera parte de la multiplicación del área de su base en la altura.
Formula volumen de pirámide

V = 1 
Ab · h
3

donde 
V
 - pirámide volumen,
Ab
 - área de las bases de la pirámide,
h
 - longitud de la altura de la pirámide.


Volumen del tetraedro regular

tetraedro regularFormula volumen de tetraedro regular

V = 
a
3√2
12


donde 
V
 - tetraedro regular volumen,
a
 - longitud de la arista del tetraedro regular.Vea también online calculadora para sacar volumen del tetraedro regular.


Volumen del cilindro

cilindroEl volumen del cilindro equivale a la multiplicación del área de su base por la altura.
    Formula volumen de cilindro
  • V = 
    π R
    2 
    h
  • V = 
    Ab h
donde 
V
 - cilindro volumen,
Ab
 - área de las bases de la cilindro,
R
 - radio de la cilindro,
h
 - longitud de la altura de la cilindro,
π = 3.141592
.Vea también online calculadora para sacar volumen del cilindro.


Volumen del cono

conoEl volumen del cono equivale a la tercera parte de la multiplicación del área de su base por la altura.
Formula volumen de cono
V = 1 
π R
2 
h
3

V = 1 
Ab h
3

donde 
V
 - cono volumen,
Ab
 - área de las bases de la cono,
R
 - radio de las bases de la cono,
h
 - longitud de la altura de la cono,
π = 3.141592
.Vea también online calculadora para sacar volumen del cono.


Volumen de la esfera

esferaEl volumen de la esfera equivale a cuatro tercias de su radio a la tercera potencia multiplicado por el número “pi”.
Formula volumen de la esfera

V = 4
π R
3
3

donde 
V
 - esfera volumen,
R
 - radio de la esfera,
π = 3.141592
.


EJERCICIOS 

Publicadas por a la/s No hay comentarios.:
Suscribirse a: Entradas (Atom)